Напишіть програму, яка застосує до вказаних матриць виграшів біматричної гри двох гравців послідовне виключення строго домінованих стратегій. Тобто, поки хоча б у одного з гравців є стратегії (хоча б одна, можна більше), строго доміновані іншими його ж стратегіями, доміновані стратегії слід вилучати; цю дію треба виконати для обох гравців; може виявлятися (а може й не виявлятися), що, внаслідок вилучення стратегій одного з гравців, для іншого гравця деякі зі стратегій, які досі не були строго домінованими, стають такими; якщо таке відбувається, їх теж слід вилучати. Див. також задачу «Домінування стратегій біматричної гри» та примітки наприкінці цієї умови.

Вхідні дані

У першому рядку через пропуск (пробіл) задано кількість стратегій першого гравця ~N~ (~2{{\leqslant}}N{{\leqslant}}12~) та кількість стратегій другого гравця ~M~ (~2{{\leqslant}}M{{\leqslant}}12~). Далі йде один порожній рядок. Наступні ~N~ рядків містять платіжну матрицю виграшів першого гравця, тобто кожен з цих рядків містить рівно ~M~ чисел, розділених одинарними пропусками (пробілами), причому ~j~-е число ~i~-го рядка являє собою виграш першого гравця у випадку, якщо перший гравець застосує стратегію №~i~, а другий стратегію №~j~. Далі йде один порожній рядок, після якого в аналогічному форматі задано матрицю виграшів другого гравця: теж ~N~ рядків по ~M~ чисел, де ~j~-е число ~i~-го рядка являє собою виграш другого гравця у випадку, якщо перший гравець застосує стратегію №~i~, а другий стратегію №~j~. Всі значення елементів матриць є цілими числами, що не перевищують за модулем (абсолютною величиною) 999.

Результати

Ваша програма повинна вивести «решти» матриць виграшів, що лишаються після викреслень, у такому вигляді: спочатку «решту» матриці виграшів першого гравця, потім другого. Кожна з цих «решт» може бути утворена таким чином: взята відповідна матриця зі вхідних даних, зліва дописані номери стратегій першого гравця a1, a2, ..., а згори номери стратегій другого гравця b1, b2, ..., після чого відбуваються власне всі викреслення. У наведених прикладах результати матриці відформатовані так, щоб створювати матриці з акуратними стовпчиками, але при автоматичній перевірці це не перевірятиметься (досить, щоб всередині кожного з рядків відповіді утворювалася та сама послідовність позначок стратегій та чисел).

Приклади

Вхід

3 2

1 2
4 8
6 4

11 12
21 22
31 32

Результат

    b2
a2  8
    b2
a2  22

Вхід

3 2

1 2
4 8
1 2

11 12
91 22
31 32

Результат

    b1
a2  4
    b1
a2  91

Вхід

3 2

1 2
4 8
6 4

11 12
29 28
31 32

Результат

    b1 b2
a2  4  8
a3  6  4
    b1 b2
a2  29 28
a3  31 32

Примітки

Перший тест передбачає, наприклад, такі перетворення:

(Тут і далі, в кожній комірці, перше число – виграш першого гравця, друге – виграш другого. Слово «наприклад» вжите в тому смислі, що існують також інші порядки викреслювань, які дають такий самий результат.)

Другий тест передбачає, наприклад, такі перетворення:

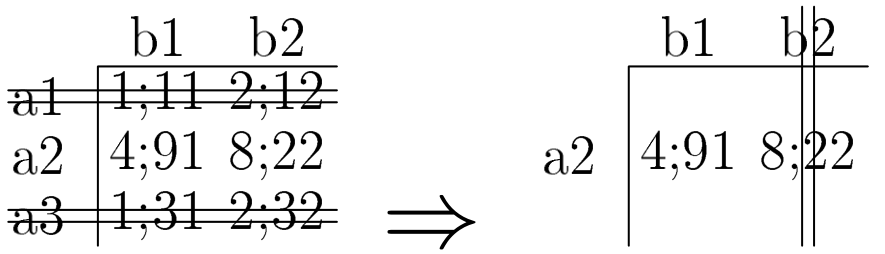
Перше викреслення правильне, бо можна, щоб і a1, і a3 одночасно були строго домінованими; тут неважливо, що вони (для 1-го гравця) однакові, досить і того, що кожну з них строго домінує a2.

У третьому тесті вдається вилучити лише стратегію a1.