Є стрічка шириною в одну клітинку і довжиною в ~N~ клітинок. Двоє грають у таку гру. Кожен з гравців на кожному своєму ході може закреслити кілька клітинок. Якщо закреслення відбувається скраю смужки, або безпосередньо поруч з уже закресленою клітинкою, то закреслити можна або 1, або 2 клітинки підряд. Якщо закреслення відбувається не згідно попереднього речення, а десь всередині досі суцільного фрагмента стрічки (так, щоб по обидва боки від закресленого були незакреслені фрагменти), то закреслити можна або 2, або 4 клітинки підряд. Ніяких інших варіантів ходу нема. Ходять гравці по черзі, пропускати хід не можна. Виграє той, хто закреслює останню клітинку (можливо, разом із ще кількома).

Напишіть програму, яка визначатиме, хто виграє при правильній грі обох гравців. Іншими словами, хто може забезпечити собі виграш, хоч би як не грав інший. Якщо виграє перший, то програма повинна знайти також сукупність усіх його виграшних перших ходів.

Пару прикладів суто для пояснення правил гри.

Повний перелік усіх можливих ходів для позиції «суцільна стрічка з 4-х клітинок»:

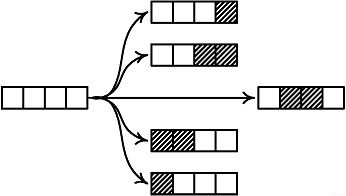
З кожного з країв можна закреслити 1 або 2 клітинки; посередині можна закреслити 2 клітинки, але не 4, бо «всередині» вимагає, щоб з кожного з країв хоч щось лишилося. Всього є 5 варіантів ходу.

Повний перелік усіх можливих ходів для позиції «10 клітинок, 3-тя та 4-та вже закреслені раніше»:

(Суцільно-чорні – закреслені раніше; заштриховані – закреслені на поточному ході.) У лівому фрагменті можна закреслити будь-яку одну крайню, або двома різними способами (дві крайні зліва чи дві крайні справа) закреслити обидві. Якщо креслити з країв правого фрагмента, виходить чотири варіанти: закреслити одну зліва, або дві зліва, або одну справа, або дві справа. Якщо креслити всередині правого фрагмента, є один варіант закреслити зразу чотири, і три варіанти закреслити дві. Всього є 11 варіантів ходу.

Вхідні дані

Єдине ціле число ~N~ (~1\leqslant N\leqslant 2000~) – початкова кількість клітинок у стрічці (спочатку – єдиному неперервному фрагменті).

Результати

Єдине ціле число, або 1 (якщо перший гравець може забезпечити собі виграш), або 2 (якщо другий). Якщо відповідь з першого рядка 2, то на цьому виведення слід припинити. А якщо відповідь з першого рядка 1, то далі треба вивести також перелік всіх можливих перших ходів першого гравця, після яких другий (при правильній грі першого) вже ніяк не зможе виграти. Цей перелік виводити в такому форматі: кожен такий хід в окремому рядку; кожен хід записується як пара чисел через пропуск: номер початкової клітинки закреслення та кількість клітинок, що закреслюються; якщо є багато різних виграшних перших ходів, вони повинні бути відсортовані за зростанням номера початкової клітинки, а якщо є багато різних виграшних перших ходів, де закреслення починаються в одній клітинці, то за зростанням кількості клітинок, що закреслюються.

Кількість перших виграшних ходів виводити не треба. Вважати, що клітинки занумеровані з одиниці: 1, 2, ..., ~N~.

Приклади

Вхід

2

Результат

1
1 2

Вхід

3

Результат

2

Вхід

4

Результат

1
1 1
2 2
4 1

Вхід

17

Результат

1
6 4
7 2
9 4
10 2

Примітки

У першому прикладі (~N{=}2~), виграшним є лише один хід: закреслити зразу обидві клітинки й виграти за один напівхід.

У друугому прикладі (~N{=}3~), виграшних ходів нема взагалі, бо виграш може забезпечити 2-й гравець. 1-й гравець не має іншого вибору, крім як креслити чи то одну, чи то дві клітинки біля одного з країв, і в будь-якому з цих випадків 2-му гравцеві дістанеться один неперервний фрагмент або з однієї клітинки, або з двох; в будь-якому разі, його можна увесь закреслити й виграти.

У третьому прикладі (~N{=}4~), виграшними є формально три різні ходи, два з яких (1 1 та 4 1) симетричні: закреслити якусь одну з крайніх клітинок, після чого супернику дістанеться один неперервний фрагмент із трьох клітинок, що призведе до програшу 2-го гравця згідно міркувань попереднього абзацу. Інший виграшний перший хід – закреслити дві клітинки рівно посередині, тоді від стрічки лишається два окремих квадратики ~1{\times}1~, суперник не матиме іншого вибору, крім як закреслити один з них, після чого перший гравець закреслює останній з цих квадратиків і виграє. Зверніть увагу, що у відповіді ходи мусять бути в порядку 1 1, 2 2, 4 1.