У цій задачі трохи інше, чим зазвичай, трактування жадібності. Тут є етап «перепробуємо такий, такий, ... варіанти, та виберемо з них максимальний» (що до певної міри протирічить ідеї жадібності). Однак, ідея, завдяки якій цей максимум не доводиться шукати серед усіх ~\Theta(N^2)~ варіантів (пари кожної стінки з кожною іншою), а вдається обійтися значно меншою кількістю варіантів (~\Theta(N)~), все ж може бути розцінена як жадібна.

Пан Скупій вирішив побудувати собі басейн. Оскільки пан Скупій дуже скупий, він намагається використати будівлю, що вже існує.

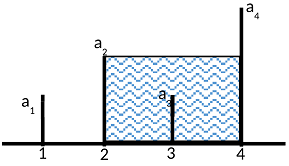
Будівля являє собою абсолютно рівний коридор одиничної ширини, в якому є ~N~ перегородок. Якщо розмістити вісь ~Ox~ вздовж коридору, усі перегородки будуть знаходитись точно в її цілочисельних координатах з кроком 1, причому в ширину (яка теж дорівнює 1) перегородки займають увесь коридор, а висоти різних перегородок можуть відрізнятися. Басейн, що створюється, повинен мати якнайбільший можливий об'єм, за умови, що з усіх існуючих перегородок потрібно залишити тільки дві та збільшувати їх висоту заборонено.

Вхідні дані

Програма зчитує в першому рядку ціле число ~N~ (~2\leqslant N\leqslant 10^5~) – кількість перегородок. Потім програма зчитує в другому рядку ~N~ цілих чисел ~a_i~ (~1\leqslant a_i\leqslant 10^9~) – висоти перегородок.

Результати

Програма виводить єдине число – максимально можливий об'єм створюваного басейна з урахуванням вказаних обмежень.

Приклади

Вхід

4
1 2 1 3

Результат

4